Table Of Content
SWTs randomly allocate clusters to groups that cross over from a control condition to an intervention at different crossover points (b). Key aspects of the allocation strategy are the number of clusters per group (d), the number of groups (e), and the length of time between successive crossover points, sometimes referred to informally as the ‘step length’ (h), which together also determine the total number of clusters (f) and total trial duration (a). We define a step in the design to be both a crossover point and the time to the subsequent crossover point (c). We developed a framework to define and report the key characteristics of a stepped wedge trial, including cluster allocation and individual participation. We also considered the relative strengths and weaknesses of trials according to this framework.
STATISTICAL CONSIDERATIONS FOR STEPPED WEDGE DESIGNS
A major change in the method used to finance healthcare in Mexico was evaluated by a phased and random implementation.8 A randomised evaluation on such a large scale represents a major achievement in the robust evaluation of a public policy. The Harvard research team was tasked with an evaluation at the request of the Mexican Ministry of Health (in the expectation that if the intervention was successful it would survive any change of government). Seventy four clusters were matched in pairs so that one received the intervention and the other acted as control (as illustrated in fig 1b). In this particular case, an undertaking was made to make the intervention available to control clusters on completion of the study.
November 29, 2023: Special Biostatistics Series Continues With Guidelines for Stepped-Wedge Trials - Rethinking Clinical Trials
November 29, 2023: Special Biostatistics Series Continues With Guidelines for Stepped-Wedge Trials.
Posted: Wed, 29 Nov 2023 08:00:00 GMT [source]
Design choice one: number and length of steps
Effects of the WHO Labour Care Guide on cesarean section in India: a pragmatic, stepped-wedge, cluster-randomized ... - Nature.com
Effects of the WHO Labour Care Guide on cesarean section in India: a pragmatic, stepped-wedge, cluster-randomized ....
Posted: Tue, 30 Jan 2024 08:00:00 GMT [source]
Four of the studies [4,12,19,21] included long term follow-up beyond the period in which stepping took place, since the outcomes to be assessed may occur at a point following the final step (i.e. there is a lag between intervention and outcome). In the Wilmink study [19], individuals cross-over from control to intervention at various points, but contribute person-years of data to both sections of the wedge. We used rapid qualitative analysis techniques,21 which start with team members debriefing after each interview and populating a structured template (Supplemental Appendix 2) that corresponded with central topics of the interview guide. During the debriefing process, team members assessed data saturation, finding no new themes after interviewing the 6th grantee.21,23 Next, data were aggregated into a matrix (Supplemental Appendix 2) to compare preliminary themes across grantees.
Three main stepped wedge cluster randomised trial designs: individual exposure and measurement
The control groups subsequently receive the intervention and further evaluation of effectiveness was undertaken, suggestive of the stepped wedge approach. The third study [12] employs what the authors term a "combined parallel/stepped wedge design", although only four out of the eight clusters crossed-over from the control to the intervention groups, with all of these clusters crossing-over at the same time. In other words, clusters are randomized to a sequence that determines when—not if—they receive the intervention, which makes the design appealing and relevant for quality improvement and practice transformation initiatives.
Authors’ contributions
The SW-CRT design does not allow for staggered recruitment; staggered recruitment prevents full randomization. Recruitment was very challenging because of this short time frame, in addition to the large volume of sites, particularly given that smaller practices tend to be independent, making them difficult to reach. The Oklahoma cooperative did not have an existing network from which to recruit and ultimately extended their initial 3-month recruitment period to 8 months. The New York City cooperative benefited from partnering with large practice networks that had existing relationships and communication and data infrastructures that allowed them to identify and contact eligible practices.
The treatment effect can be optimally assessed under the assumption of an identical correlation at all time points. A method is available to calculate the power and the number of clusters that would be necessary in order to achieve statistical significance by the appropriate type of significance test. All of the statistical techniques presented here are based on the assumptions of a normal distribution of cluster means and of a constant intervention effect across all time points of measurement. Select summary of sample size methods for stepped wedge cluster randomized trials and related software.

Stepped wedge designs can be attractive to study intervention programs aiming to improve the delivery of patient care, especially when examining a small number of heterogeneous clusters. CB and RL designed the study, CB undertook the literature searching, data extraction and analysis and CB and RL drafted the manuscript. Cook and Campbell were possibly the first authors to consider the potential for experimentally staged introduction in a situation when an innovation cannot be delivered concurrently to all units [3].
Reporting of stepped wedge cluster randomised trials
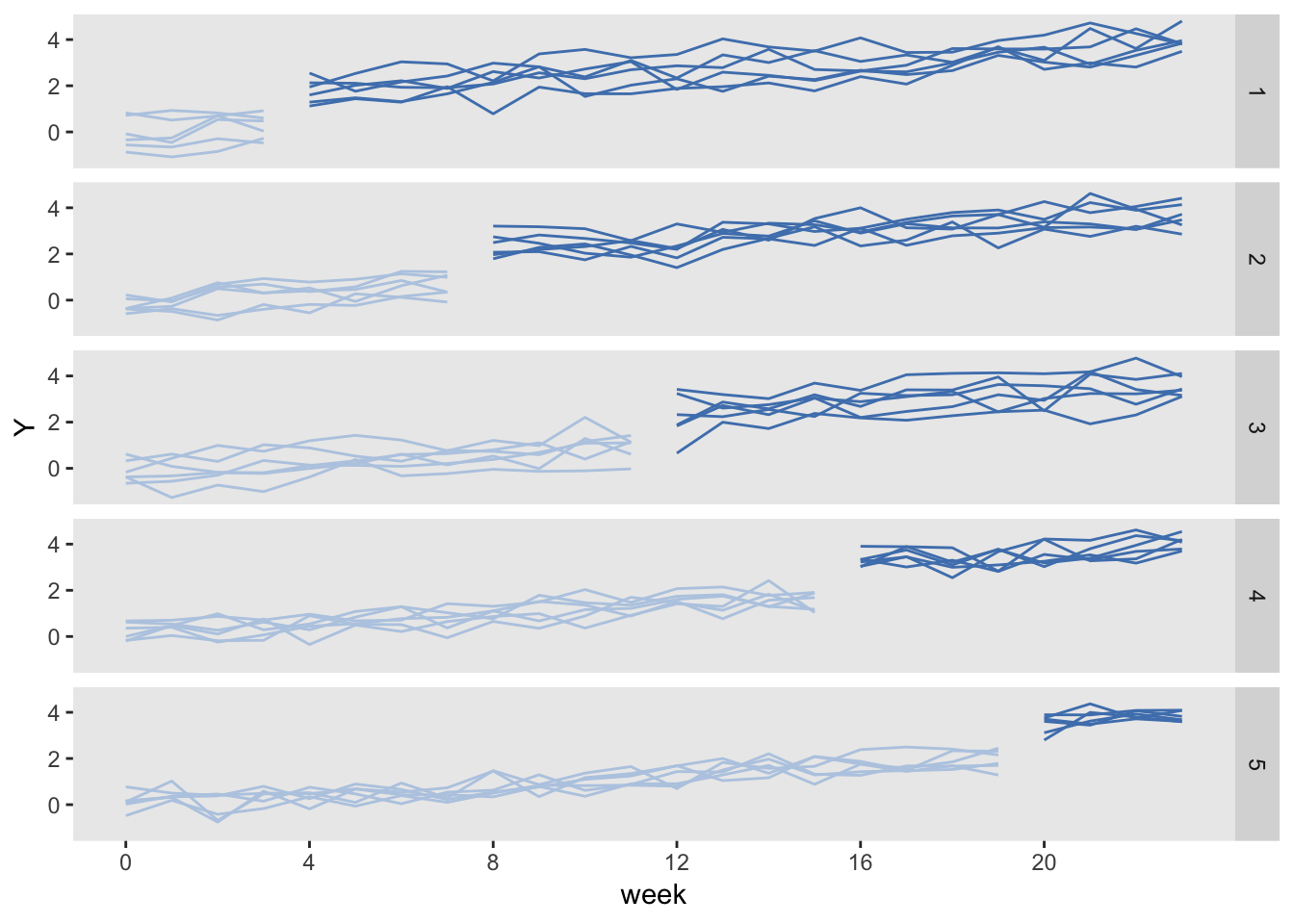
At least in the case of cross-sectional sampling and standard analysis methods, greater power is achieved with a higher number of steps [7], reaching a maximum when the size of each group is one cluster. Furthermore, in some trials it may be impossible to implement the intervention in more than one cluster at a time. However, conversely in other trials logistical constraints may prevent this, for example because each crossover point may induce training or other costs. In a closed cohort or open cohort SWT it is often desired to take measurements just before each crossover point, so a high number of steps may imply more measurement points and hence greater costs.
Challenges
Individuals visiting the clinic/ward once it has crossed-over to intervention will then contribute data to the intervention section of the wedge. The SW-CRT design has strict randomization requirements; all practices must be enrolled before randomization, and practices are assigned to staggered start dates. The Northwest cooperative learned from prior experience with SW-CRTs that sites often want to start sooner rather than later or would not join unless they received an early intervention. This was one reason why that cooperative chose the 2×2 factorial design, which allows all sites to begin the intervention at the same time. The North Carolina cooperative had a different experience, in which sites wanted to start later than when they were assigned, owing to staffing or EHR changes.
He is also a faculty member at the Yale Center for Methods in Implementation and Prevention Science, and Yale Center for Analytical Sciences. He has a Ph.D. in biostatistics from Duke University, and his main research interests include methods for designing and analyzing cluster randomized trials, methods for addressing missing data, and methods for estimating causal effects with observational studies. Importantly, we have noted that in some SWTs outcome data are collected a long time before or after rollout, and then included in the primary analysis, such as in case study three. We think that this is generally inadvisable [14], and recommend collecting such data only if this does not reduce the data collected during the rollout period. Furthermore we suggest these data should be used only in an informal assessment of how the intervention changed the time trend of the outcome seen before rollout, or of whether the intervention effect is sustained beyond the rollout period. We recommend first investigating constraints on the number of steps and the minimum suitable step length given the lag period.
As the number and type of undetected cases will likely affect response to intervention there can be carry-over effects, most clearly in a closed cohort but also in an open cohort, unless individuals leave and join clusters at a high rate. This may be a concern in trials, such as one addressing detection and improved management of patients with multiple comorbidities and medications found in our review [25], or another trial involving identifying and treating depression in nursing homes [26]. This problem of changing participant distribution over time is most obvious for time-to-event outcomes such as death, and analysis of the intervention effect will be subject to survivor bias. Few (or even no) individuals participate as the trial begins, but more become eligible and participate over time, and are then exposed for a short period. The middle participant is exposed only to the control condition, although the outcome is recorded after the cluster has crossed over to the intervention condition.
If statistical analysis of the trial is performed correctly (and at an appropriate level of complexity), basic methodological requirements can be met. Although the conditions required for a valid statistical evaluation of the treatment effect can be specified clearly in theory, in practice they are difficult to test. The basic principles of the stepped wedge design and related statistical techniques are described here on the basis of pertinent publications retrieved by a selective search in PubMed and in the CIS statistical literature database. In a cohort design, some acknowledgment for the dependence between individual measurements over the course of the study will be needed. The simplest option is perhaps to introduce an additional random effect for individuals in the study (as in example 3). The Matching Michigan study identified secular trends and no evidence of any intervention effect, even though at first the intervention looked to be a success.
However, SWTs encompass a broad range of designs, and the methodological literature is lagging behind the growth in the conduct of SWTs. Much of the literature to date has focussed on a small range of SWT designs where data are collected from individuals at discrete time points, and individuals contribute one measurement during the study [2–5]. This may, for example, arise from cross-sectional sampling from all clusters just before each crossover point (whenever a group of clusters changes from control to intervention condition). However, most SWTs described in the recent literature do not follow this particular design [1].

No comments:
Post a Comment